Aplicación
de la teoría de colas
Una
vez ya estemos familiarizados con los conceptos en torno a esta teoría y los
elementos que la componen, es hora de aplicar esta teoría con las fórmulas que
arrojarán resultados puntuales en cuanto la optimización de procesos.
Los
elementos que intervienen en la teoría de colas se representan como variables
para cada una de las formulas, de esta manera:
μ
tasa de servicio a los clientes
|
L
numero esperado o estimado de clientes en el sistema
|
Lq
numero esperado o estimado de clientes que están en la cola
|
W
tiempo esperado o estimado en el sistema
|
Wq
tiempo esperado o estimado en la cola
|
Po
probabilidad de que no existan clientes en el sistema
|
λ Tasa
de llegada de clientes
|
Pn
probabilidad de tener n clientes en el sistema (n clientes en el servidor)
|
ρ
probabilidad de que la facilidad del servicio este siendo utilizada
|
C
número de canales o servicios
|
K
tamaño de la población finita.
|
 |
Tabla de
fórmulas, Autor:S. Urrutia Facultad de Ingeniería | Universidad Nacional del
Centro de la Provincia de Buenos Aires http://www.fio.unicen.edu.ar/usuario/surrutia/a5-1/index_archivos/Material%20Adicional/flatc.pdf
|
Los valores de tiempo, siempre deben estar en las mismas unidades.
El tiempo de llegada es : 1/ λ
Tiempo de atención: 1/ μ
Como se quiere simular un sistema de colas básico se debe poder simular la llegada de las solicitudes, la que generalmente se hace con una distribución de Poisson 
que esta se da cuando un cliente llega a la cola durante un intervalo de tiempo, siempre existe la probabilidad de que llegue un cliente, dentro de un intervalo de tiempo dado y fijo por lo tanto la llegada de un cliente no debe influenciar en la de otro, ya que siempre llegará dentro de un intervalo de tiempo.
que esta se da cuando un cliente llega a la cola durante un intervalo de tiempo, siempre existe la probabilidad de que llegue un cliente, dentro de un intervalo de tiempo dado y fijo por lo tanto la llegada de un cliente no debe influenciar en la de otro, ya que siempre llegará dentro de un intervalo de tiempo.
o una distribución exponencial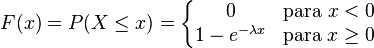 
, para los sistemas sencillos.
, para los sistemas sencillos.
También existen otro tipo de distribución como el de Erlang 
Esta distribución alimentaría al sistema de una serie de solicitudes, pero no se le proporciona al sistemas valores también de atención que varíen, por lo que se asume que la tasa de atención es una sola. De esta manera limita un poco simular de una manera real, porque no siempre se atiende a los clientes con la misma velocidad, sino que varía, para este tipo de situaciones, existe la Simulación Montecarlo que genera variables al azar para tanto la llegada como la atención. El tiempo de atención también puede ser modelado por medio de Poisson por ejemplo.
Conclusión
Por medio de estos estudios y multiples simulaciones se puede observar y analizar mas los comportamientos en una cola como por ejemplo, costos, tiempos, cantidades de servidores, valores que se pueden extraer, analizar y luego actuar para sacar el beneficio que uno esta esperando.
excelente
ResponderEliminar