Video de Teoría de Colas

Qué es la Teoría de Colas

¿Qué es la teoría de colas?

La teoría de colas es un conjunto de operaciones y de modelos matemáticos que nos ayuda en el estudio del comportamiento de las colas. Probablemente usted se estará preguntando ¿a qué nos referimos con cola? Bueno, una cola es una línea de espera en la cual se encuentra un “cliente” en un lugar esperando ser atendido por un “servidor”, el cual es capaz de brindarle alguna especie de servicio al cliente. Probablemente, usted hace colas todos los días, por ejemplo, cuando se encuentra en un banco o cuando está en una cafetería, en estas situaciones usted (cliente) se encuentra haciendo fila (cola) para poder ser atendido por el cajero (servidor).

¿Cuál es la utilidad de la teoría de colas?

La teoría de colas se utiliza cuando se necesita saber o analizar el comportamiento de una cola, ya sea para reducir costes en un sistema, o para agilizar el proceso de atención a un cliente, o para sacar estadísticas. Sea cual sea la razón, las ecuaciones matemáticas y los modelos matemáticos nos ayudan a saber estas cosas.

¿Cuáles son los elementos existentes en un modelo de colas?

• Población: Son el conjunto de personas o individuos que tienen la posibilidad de llegar a solicitar algún servicio en cuestión. Existen dos tipos de población: la finita y la infinita.
  
  
• Cliente: Es la persona o individuo de la población que solicita el servicio.
  
  
• Capacidad de la cola: Esto es la cantidad máxima de clientes que la cola puede contener antes de empezar a dar servicios.
  
  
• Disciplina de la cola: Es la manera en que los clientes son seleccionados para ser atendidos por el servidor. Los métodos o disciplinas más comunes son la FIFO (el primero que llega es el primero que sale), la LIFO (el último que llega es el primero que sale) y la RSS (selección random de clientes).
  
  
• Mecanismo de Servicio: Esto son los procedimientos que dictan cómo se le da a los clientes el servicio que han solicitado.
  
  
• La cola: este término propiamente dicho, es la colección o grupo de los clientes que están en espera esperando a ser atendidos.
  
  
• El sistema de cola: es el conjunto formado por la cola y el mecanismo de servicio, junto con la disciplina de la cola, que es lo que nos indica el criterio de qué cliente de la cola elegir para pasar al mecanismos de servicio.

Analisis de cola

Analisis de cola
Winqsb, que es un programa que ayuda a resolver, mostrar y evaluar los comportamientos de los sistemas de colas y asi determinar los costos del sistema. El mismo sistema en si trae un modulo para efectuar dicho proceso.
¿Que sistemas de colas se pueden analizar?
Se analizan sistemas donde existe uno o multiples canales o servidores, la poblacion o cantidad de clientes es finita o infinita con un modelo de llegada especificado, es decir su distribucion, la longuitud puede ser limitada como ilimitada.
Para poder evaluar mediante este programa incluye el numero de clientes en el sistema, promedio, numero de clientes en un servicio ocupado, el tiempo total promedio que pasa en el sistema, probabilidad de que el servicio este desocupado, algunos costos entre otros.
Este software es de mucha utilidad a la hora de simular para determinar estos comportamientos, y tomar ciertas medidas de correccion.

Notacion de Kendall

Notacion de Kendall
David Kendall introdujo una notacion que permite describir las colas y mostrar las caracteristicas de las mismas, mas que nada clasificar los diferentes tipos de colas.
De forma general se tiene que se determina de la siguiente manera:

A/B/C/D/E/F

Ahora bien estas letras representan diferentes criterios que se explica a continuación:
A representa el tipo de distribucion de probabilidad para el proceso de llegada, es decir los patrones
B representa el tipo de distribuccion de probabilidad para el proceso de servicio o atencion
C representa el numero de servidores o canales dentro del sistema
D representa el numero maximo de clientes que son permitido en el sistema de colas, ya sea que esten esperando o que esten adquiriendo el servicio, es decir por partes
E indica la capacidad del Sistema en general
F representa la poblacion

Estos simbolos a su vez pueden adoptar diferentes valores:
Para A se presentan los siguientes:
GI indica que existe una distribuccion de llegada con tiempo promedio entre ambos, es decir que es general
D: se usa para expresar valores deterministicos con tiempo promedio constantes
M: indica que existe una distribucion de llegada tipo Poisson, y que es independiente de la llegada anterior. Con esto hablamos de distribucion tipo exponecial entre los tiempos entre llegadas
EK: para indicar que existe una distribuccion tipo Erlang, esto representa que los datos se agrupan estrechamente alrededor de la media, promedio

Ahora los valores que toma B son los siguientes:
G: para indicar que existe una distribuccion general, hablando desde el punto de vista de los tiempo de servicio
D: representa un tipo de distribucion deterministico
M: indica que se usa distribucion tipo exponecial para general los tiempos de servicios
Ek: esta compuesta de k numeros de tareas donde cada una tiene un servicio exponencial identico

Para C se toma el número de facilidades que ofrece el servicio, o las unidades de servicio, mientras que D admite cualquier tipo de disciplina LIFO, FIFO, PRI, SIRO o GD
E toma el valor de los clientes que son admitidos en el sistema, si no hay restricciones se asume que es infinito, igual para F que toma el total de los clientes que pueden requerir el servicio en un determinado espacio de tiempo, de lo contrario se establece que es infinito.

Aplicación de la teoría de colas

Aplicación de la teoría de colas

Una vez ya estemos familiarizados con los conceptos en torno a esta teoría y los elementos que la componen, es hora de aplicar esta teoría con las fórmulas que arrojarán resultados puntuales en cuanto la optimización de procesos.

Los elementos que intervienen en la teoría de colas se representan como variables para cada una de las formulas, de esta manera:

μ tasa de servicio a los clientes	L numero esperado o estimado de clientes en el sistema	Lq numero esperado o estimado de clientes que están en la cola
W tiempo esperado o estimado en el sistema	Wq tiempo esperado o estimado en la cola	Po probabilidad de que no existan clientes en el sistema
λ Tasa de llegada de clientes	Pn probabilidad de tener n clientes en el sistema (n clientes en el servidor)	ρ probabilidad de que la facilidad del servicio este siendo utilizada
C número de canales o servicios	K tamaño de la población finita.

Tabla de fórmulas, Autor:S. Urrutia Facultad de Ingeniería | Universidad Nacional del Centro de la Provincia de Buenos Aires http://www.fio.unicen.edu.ar/usuario/surrutia/a5-1/index_archivos/Material%20Adicional/flatc.pdf

Los valores de tiempo, siempre deben estar en las mismas unidades.

El tiempo de llegada es : 1/ λ

Tiempo de atención: 1/ μ

Como se quiere simular un sistema de colas básico se debe poder simular la llegada de las solicitudes, la que generalmente se hace con una distribución de Poisson   que esta se da cuando un cliente llega a la cola durante un intervalo de tiempo, siempre existe la probabilidad de que llegue un cliente, dentro de un intervalo de tiempo dado y fijo por lo tanto la llegada de un cliente no debe influenciar en la de otro, ya que siempre llegará dentro de un intervalo de tiempo.

o una distribución exponencial 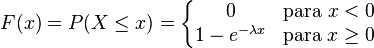, para los sistemas sencillos.

También existen otro tipo de distribución como el de Erlang 

Esta distribución alimentaría al sistema de una serie de solicitudes, pero no se le proporciona al sistemas valores también de atención que varíen, por lo que se asume que la tasa de atención es una sola. De esta manera limita un poco simular de una manera real, porque no siempre se atiende a los clientes con la misma velocidad, sino que varía, para este tipo de situaciones, existe la Simulación Montecarlo que genera variables al azar para tanto la llegada como la atención. El tiempo de atención también puede ser modelado por medio de Poisson por ejemplo.

Conclusión

Por medio de estos estudios y multiples simulaciones se puede observar y analizar mas los comportamientos en una cola como por ejemplo, costos, tiempos, cantidades de servidores, valores que se pueden extraer, analizar y luego actuar para sacar el beneficio que uno esta esperando.